Satelity

Pierwsza prędkość kosmiczna

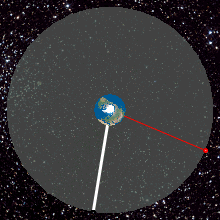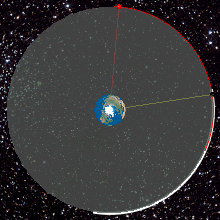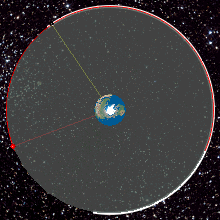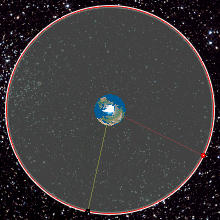
Jest to prędkość jaką trzeba nadać ciału na powierzchni planety, aby pokonując jej grawitację stało się sztucznym satelitą. Pierwsza prędkość kosmiczna wyliczana jest dla orbity kołowej tuż przy samej powierzchni. W rzeczywistości, aby uzyskać satelitę musimy wynieść ciało wysoko poza atmosferą, po to aby nie uderzyło w jakąś przeszkodę i żeby opór powietrza nie zwalniał prędkości jego ruchu. Na rysunku pocisk wystrzelony z pierwszą prędkością kosmiczną osiąga kołową orbitę oznaczoną literą C. Wynosi ona około 7,9 km/s.

Druga prędkość kosmiczna

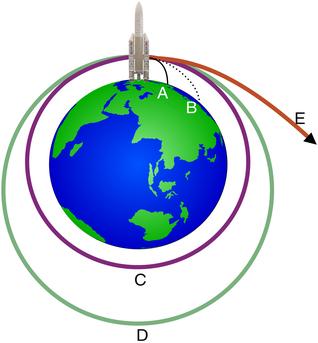Druga prędkość kosmiczna to prędkość jaką trzeba nadać ciału, aby na zawsze opuściło planetę. Dla Ziemi prędkość ta wynosi około 11,2 km/s. Ciało, może zostać rzucone pod dowolnym kątem do powierzchni Ziemi, byle tylko w nią nie uderzyło. Jego trajektoria staje się wtedy paraboliczna. Taką trajektorią ma tor E

Trzecia prędkość kosmiczna

Opuszczenie Układu Słonecznego wymaga znacznie większej prędkości ponieważ ciało musi pokonać grawitację Słońca. Tę prędkość nazywamy 3 prędkością kosmiczną.

Satelita meteorologiczny

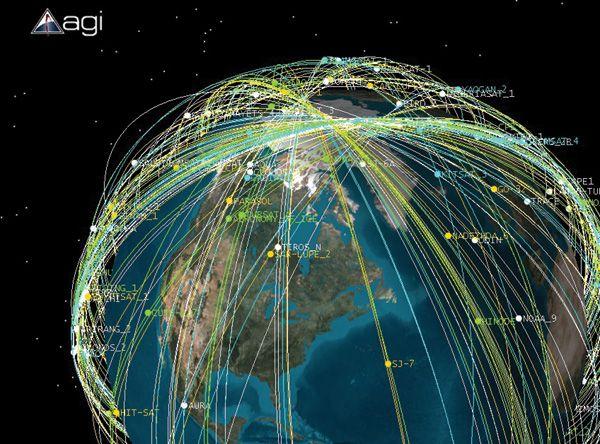Satelity meteorologiczne i podobne fotografujące i szpiegowskie poruszają się na bardzo niskich orbitach nawet na wysokości 100 km. Przelatują zazwyczaj w okolicach biegunów a ich czas obiegu Ziemi to kilka godzin. Dzięki szybkiemu ruchowi i obrotowi Ziemi wokół własnej osi potrafią sfotografować lub zbadać jej powierzchnią w krótkim czasie.

Satelita geostacjonarny

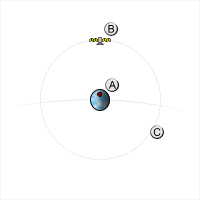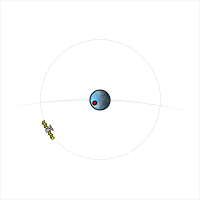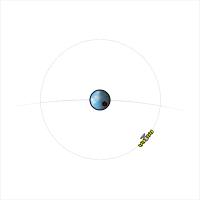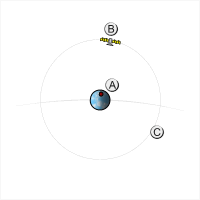Satelita ten porusza się wokół Ziemi nad jej równikiem w taki sposób, że w każdej chwili znajduje się nad tym samym punktem nad Ziemią i wydaje się jakby nie poruszał się. Satelity te służą do przekazywania sygnałów telewizyjnych i znajdują się około 42 000 km od środka Ziemi.

Satelity systemu GPS

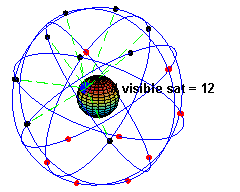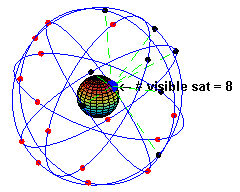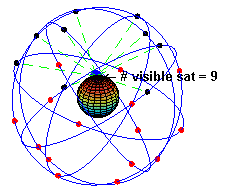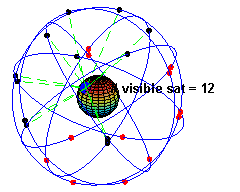System GPS - Global Positioning System to system służący do nawigacji wykorzystujący w tym celu sieć satelitów krążących nad Ziemią. Obecnie jest ich ponad 30. Orbity tych satelitów są kołowe i muszą być tak ułożone, aby w każdej chwili nad danym punktem na Ziemi znajdowało co najmniej kilka z nich. Aby korzystać z systemu musimy posiadać urządzenie potrafiące wykorzystać sygnały wysyłane przez satelity GPS. Mierząc czas dotarcia sygnału z kilku satelitów do naszego odbiornika, może on wyliczyć nasze położenie na Ziemi. Odbiorniki nie wysyłają żadnych sygnałów do satelitów, a jedynie dobierają. Kluczowym w precyzji pomiaru jest dokładność czasu i znajomość położenia tych satelitów.

III prawo Keplera w ruchu po okręgu

Jest to uproszczona wersja III prawa Keplera.
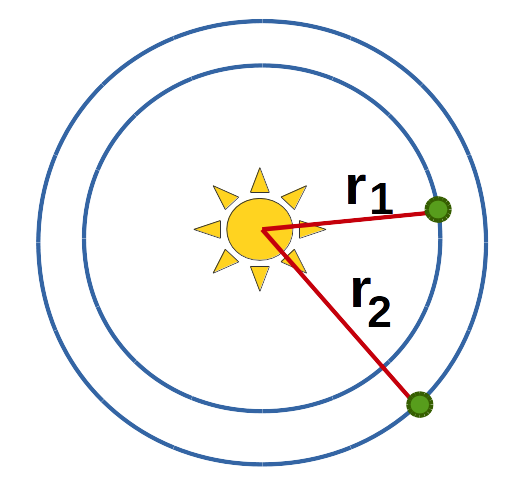Iloraz okresu obiegu (czas wykonania jednego pełnego okrążenia) satelity (naturalnego lub sztucznego) podniesiony do kwadratu do odległości satelity od ciała wokół którego krąży jest wielkością stałą dla danego układu.

$\frac{T_{1}^{2}}{r_{1}^{3}} = \frac{T_{2}^{2}}{r_{2}^{3}}$

Dlatego pokazany na rysunku drugi satelita będzie mieć ten sam stosunek kwadratu okresu do trzeciej potęgi promienia jak pierwszy.

Prawa Keplera, a prawa dynamiki

Wszystkie prawa Keplera da się wyjaśnić z zasad dynamiki i prawa grawitacji. W ruchu po okręgu siła dośrodkowa jest równa sile grawitacji (jest niż siła grawitacji): $G \cdot \frac {m \cdot M}{r^2} = \frac {m \cdot v^2} {r} $ więc skracając i przekształcając:

$G \cdot \frac {M}{r} = v^2$

Prędkość w ruchu planety możemy wyliczyć z okresu obiegu jako $v = \frac {2 \pi \cdot r } {T}$. P

odstawiając to za v w poprzednim wzorze i przekształcając otrzymamy III prawo Keplera:

$\frac {T^2}{r^3} = \frac {4 \pi^2} {G \cdot M} = const$ wraz ze stałą.

Wyznaczanie mas ciał niebieskich

Z wzoru na III prawo Keplera: $\frac{T^{2}}{r^{3}} = \frac{4 π^{2}}{G \cdot M}$ możemy obliczyć masę ciała znajdującego się w środku. Należy zmierzyć tylko okres obiegu i promień (w ruchu po elipsie półoś wielką) ruchu jakiegoś satelity tego ciała. Trudniej jest zmierzyć masę ciała wokół którego nie krąży, żaden satelita. W prawach Keplera masa satelity nie ma wpływu na parametry orbity ruchu. Tak samo w spadku swobodnym przyspieszenie ciała nie zależy od jego masy.