
- Temat: Promieniowanie atomu wodoru







Według Bohra elektron krąży wokół jądra przyciągany przez siłę elektrostatyczną protonu. Siła ta pełni rolę siły dośrodkowej w ruchu elektronu po okręgu. Jednak elektron krążąc wokół jądra nie wypromieniowuje z tego powodu energii (choć tak by wynikało z praw fizyki klasycznej).
1. Musiał dodatkowo założyć, że elektrony mogą tylko ściśle określone momenty pędów, przez co mogą zajmować tylko dokładnie określone orbity (i odległości od jądra).
gdzie moment pędu to:
2. Elektrony mogą przeskakiwać między orbitami, a różnica energii tych orbit równa jest energii wyświecanego promieniowania.
 Elektron może znajdować się tylko na jednej z orbit, a na każdej orbicie ma inną wartość energii.
Elektron może znajdować się tylko na jednej z orbit, a na każdej orbicie ma inną wartość energii.
Elektron zmieniając orbitę z niższej na wyższą musi pobrać energię równą dokładnie różnicy energii na tych orbitach:
ΔE = En - Ek
Przy spadaniu elektronu na niższą orbitę elektron oddaje taką samą energię jak przy ruchu w przeciwną stronę.
W pierwszym przypadku elektron pochłania foton, a w drugim wytwarza, ale jego energia: Ef = h · f = ΔE
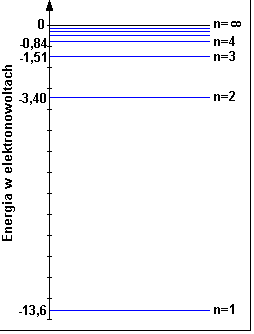 Energia elektronu na n-tej orbicie wyraża się wzorem:
Energia elektronu na n-tej orbicie wyraża się wzorem:
E0 to energia stanu podstawowego czyli to samo co E1. Wartość stałej E0 = 13,6eV
Energia ta jest ujemna ponieważ elektron wpada jakby do studni energetycznej (pomyśl o numerach poziomów parkingów podziemnych w centrum handlowym)
Foton pochłonięty lub wyemitowany przez elektron jest dokładnie równy różnicy energii przejścia między dwoma orbitami:
Foton o nieco większej lub mniejszej energii nie spowoduje przeskoku i nie zostanie pochłonięty.
Zazwyczaj elektron przebywa na pierwszej orbicie, jest to stan podstawowy atomu. Gdy pochłonie foton przechodzi na wyższe orbity i wtedy jest w stanie wzbudzonym.
Balmer odkrywając drugą serię widmową odgadł wzór na obie serie. Po odkryciu następnych linii wyznaczono doświadczalny (empiryczny) wzór na długość emitowanych fal:
Gdy porównamy ten wzór z poprzednim wyznaczymy, że stała Rydberga to:
/